楽天証券の口座でデイトレの自動売買に挑戦しようと Windows / Excel 上で利用できる マーケットスピード II RSS を活用して Python であれこれ取り組んでいます。この「自動売買への道」のトピックでは、プログラミングの話題にも踏み込んで、日々の活動をまとめています。
デイトレ用自作アプリ
以下は株価・取引に関連する情報の流れを示しています。
楽天証券では、Python からネットワーク越しに直接取引できるような API が提供されていないので、マーケットスピード II RSS を介して取引をする構成を取っています。
移動範囲 MovingRange, MR ── エントリの抑制
今回は長めの記事ですが、うまくいかなかった事例をまとめています。
デイトレで、ボラティリティが少ない局面でエントリを抑制するために、今までは移動範囲 MR で、単純なしきい値を設定していました。ただ、いまひとつ使い難いです。例えば、だらだら株価が上昇あるいは下降するトレンドでは、MR は小さくなってしまって、効果的にエントリを抑制する、あるいはエントリ可能な領域を確保する指標としては機能してくれません。
リアルタイムの取引シミュレーション (Simulated Trade) で運用している移動範囲 MovingRange クラスを下記に示しました。
class MovingRange:
def __init__(self, window_size: int):
self.window_size = window_size
self.data = deque()
self.max_q = deque() # 単調減少キュー(先頭が最大)
self.min_q = deque() # 単調増加キュー(先頭が最小)
def clear(self):
self.data.clear()
self.max_q.clear()
self.min_q.clear()
def update(self, value: float) -< float:
# 新しい値を追加
self.data.append(value)
# --- 最大値キュー更新 ---
while self.max_q and self.max_q[-1] < value:
self.max_q.pop()
self.max_q.append(value)
# --- 最小値キュー更新 ---
while self.min_q and self.min_q[-1] > value:
self.min_q.pop()
self.min_q.append(value)
# 古い値を削除(window_size を超えたら)
if len(self.data) > self.window_size:
old = self.data.popleft()
if old == self.max_q[0]:
self.max_q.popleft()
if old == self.min_q[0]:
self.min_q.popleft()
# 移動範囲を返す
return self.max_q[0] - self.min_q[0]
余談ですが、Microsoft Copilot とのやり取りで「シャドートレード」という良さげな語が出てきたので、それを動名詞にした「シャドートレーディング」を今まで使用していた Dry Run から乗り換えて使い始めました。念の為、Microsoft Copilot にこの語の用法が適切かどうかを確認しました。すると、
英語の本来の意味
shadow trading は、米国の証券規制文脈で「関連銘柄を使ったインサイダー取引」を指す専門用語。
shadow trade は一般的な英語ではあまり使われない。
なんと、適切な語ではないということが判りました。
では、Dry Run はどうかというと、
Dry Run
- 本来は「手順確認」「実行テスト」の意味
- プログラミングや DevOps では一般的
- 取引の文脈ではやや技術寄りで、金融っぽさは薄い
- 「実際の市場データでリアルタイムに走る」ニュアンスは弱い
👉 “実行前のテスト” という印象が強い
う〜ん、そう言われると、Dry Run も使いたいと思わなくなってしまいました。
それでは、英語で最もネイティブに自然で誤解がないのは何かというと、下記の語にたどり着きました。
Simulated Trade:
A real-time execution of trading logic using live market data, without generating actual orders or financial transactions.
そんなわけで、しばらくは「リアルタイムの取引シミュレーション (Simulated Trade)」と表現することにします。
Capped Trend Accumulator, CTA(仮称)
ティックデータならではのボラティリティの指標を作れないかと Microsoft Copilot と議論を重ねたところ、「一定期間のティックデータの変化量の(符号を含む)合計」の絶対値を取る方法にたどりつきました。これであれば緩やかな上昇あるいは下降トレンドの局面でそれほど値が小さくならないことを期待しました。
呼び名を Microsoft Copilot にいくつか提案してもらいました。値動きのスパイク除去をあらわす Capped から始まる Capped Trend Accumulator, CTA をとりあえずの呼称にしました。
以下に CappedTrendAccumulator クラスを示しました。
class CappedTrendAccumulator:
def __init__(self, window_size: int, cap: float = 2.0):
"""
window_size: 直近何個の価格変化イベントを保持するか
cap: 1イベントあたりの最大変化量(スパイク除去用)
"""
self.window_size = window_size
self.cap = cap
self.events = deque()
self.sum_events = 0.0
self.last_price = None
def update(self, price) -< float:
if self.last_price is None:
self.last_price = price
return 0.0
diff = price - self.last_price
clipped_diff = max(min(diff, self.cap), -self.cap)
self.events.append(clipped_diff)
self.sum_events += clipped_diff
self.last_price = price
if len(self.events) < self.window_size:
removed = self.events.popleft()
self.sum_events -= removed
return abs(self.sum_events)
値動きのスパイク状の変動は self.cap の大きさに収まるようにクリッピングしています。
MR と CTA
昨年の大納会の日に収集したティックデータで MR と CTA を評価しました。
下記のように Time 列のタイムスタンプを時刻形式に直してインデックスにした Pandas のデータフレーム df を利用します。
window_size = period = 30 で MR と CTA のインスタンスを生成して、ティックデータのデータフレームに MR と CTA 列を追加しました。短周期と長周期の移動平均 MA1 と MA2 も追加していますが詳細は割愛します。
# MR and CTA period = 30 mr = MovingRange(window_size=period) df["MR"] = [mr.update(v) for v in df["Price"]] cta = CappedTrendAccumulator(window_size=period) df["CTA"] = [cta.update(v) for v in df["Price"]]
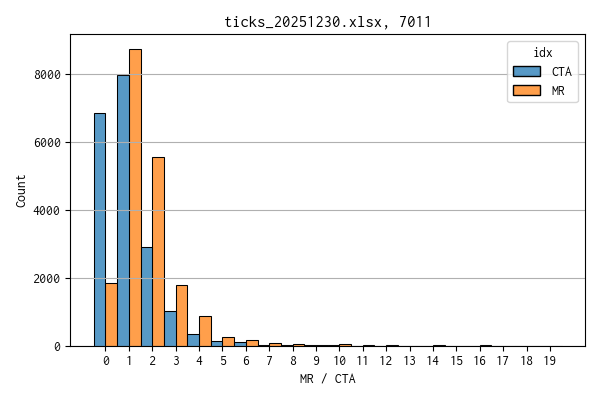
MR と CTA の分布
まずは MR と CTA の分布をヒストグラムにして比較しました。Python のコードは割愛します。
分布形状は CTA の方が 0 に寄った感じですが、具体的に数値で表すために、下記のコードを使って L1距離 と オーバーラップ係数 を算出しました。
def compare_raw_distributions(df, col_mr="MR", col_cta="CTA", bins=None):
import numpy as np
mr = df[col_mr].values
cta = df[col_cta].values
# ビンが指定されていなければ自動生成(整数ビン)
if bins is None:
low = int(min(mr.min(), cta.min()))
high = int(max(mr.max(), cta.max())) + 1
bins = np.arange(low, high + 1)
# ヒストグラム化
hist_mr, _ = np.histogram(mr, bins=bins)
hist_cta, _ = np.histogram(cta, bins=bins)
# 確率分布に正規化
p_mr = hist_mr / hist_mr.sum()
p_cta = hist_cta / hist_cta.sum()
# 指標
L1 = np.abs(p_mr - p_cta).sum()
overlap = np.minimum(p_mr, p_cta).sum()
return L1, overlap, bins, p_mr, p_cta
compare_raw_distributions(df)
(np.float64(0.5140917506685866),
np.float64(0.7429541246657068),
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20]),
array([9.45793047e-02, 4.48673113e-01, 2.85023658e-01, 9.13906604e-02,
4.44867311e-02, 1.34745937e-02, 9.00020572e-03, 3.85723102e-03,
2.52005760e-03, 1.13145443e-03, 1.85147089e-03, 1.69718165e-03,
5.65727217e-04, 1.02859494e-04, 3.60008229e-04, 2.05718988e-04,
4.62867723e-04, 2.57148735e-04, 2.57148735e-04, 1.02859494e-04]),
array([3.51522321e-01, 4.09689364e-01, 1.49969142e-01, 5.30240691e-02,
1.84632792e-02, 7.35445382e-03, 5.04011520e-03, 1.74861140e-03,
1.13145443e-03, 7.20016458e-04, 4.11437976e-04, 1.02859494e-04,
2.05718988e-04, 2.05718988e-04, 3.08578482e-04, 1.02859494e-04,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00]))
L1距離 と オーバーラップ係数 をまとめると、
- L1距離 = 0.514...
- 半分くらいはズレている
- L1距離は「分布のズレ量」を表す指標。
- 0 → 完全一致
- 0.2〜0.3 → まあまあ似ている
- 0.5 前後 → 似ている部分もあるが、違いも明確
- 1.0 以上 → かなり違う
- オーバーラップ係数 = 0.742...
- 74% は似ているが、26% はどちらか一方にしか存在しない
- オーバーラップ係数は「どれだけ重なっているか」。
- 1.0 → 完全一致
- 0.9 → ほぼ同じ
- 0.7〜0.8 → 似ている部分も多いが、違いもある
- 0.5 → 半分しか重ならない
それなりに分布の違いを確認できたので、今度は MR と CTA に対して、しきい値を設定して、エントリに関して効果的に利用できるかどうか確認しました。。
しきい値とエントリ
「しきい値を設定して、エントリの抑制に効果的に利用できるかどうか」については、少し欲張りな期待を持っています。
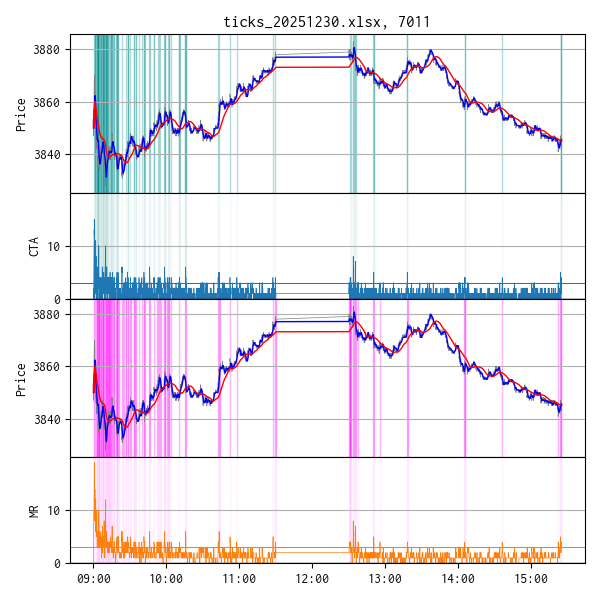
下のチャートは、CTA, MR それぞれについて、しきい値以上の時はエントリ可能な領域として、シアン、マゼンタの縦線を入れています。それぞれお上段は値動きのトレンド(灰色)に短周期と長周期の移動平均を青と赤の線で重ねています。
前場、寄り付き後の大きめの変動では、MR でもエントリ抑制は効かせられますし、現在利用している移動平均のクロス・シグナルとの相性も良くて、エントリ可能な領域も確保できています。しかし、後場に良く見られる、だらだらと上昇あるいは下降するという局面では、MR の値は小さいままで過剰にエントリを抑制する方向に効いてしまっています。
そこで今回、だらだらとした上昇あるいは下降トレンドでエントリ領域を確保できるような指標ができないかと期待して CTA という指標を定義して評価しました。
MR と CTA の分布に違いを確認できましたが、しきい値やデータをいろいろ変更して確認してみた限りでは、前述の期待を叶えられるような特性を見い出せませんでした。
今後 CTA の考え方を改良して、モノになるような指標になるかもしれないので、うまくいかなかった事例を敢えてまとめておくことにしました。
なお MR についても、ひとまず利用を止めて、エントリ判断を他の基準で試すことにします。
参考サイト
- マーケットスピード II RSS | 楽天証券のトレーディングツール
- マーケットスピード II RSS 関数マニュアル
- 注文 | マーケットスピード II RSS オンラインヘルプ | 楽天証券のトレーディングツール
- Gymnasium Documentation
- Stable-Baselines3 Docs - Reliable Reinforcement Learning Implementations
- Maskable PPO — Stable Baselines3 - documentation
- PyTorch documentation
- PythonでGUIを設計 | Qtの公式Pythonバインディング
- Python in Excel alternative: Open. Self-hosted. No limits.
- Book - xlwings Documentation


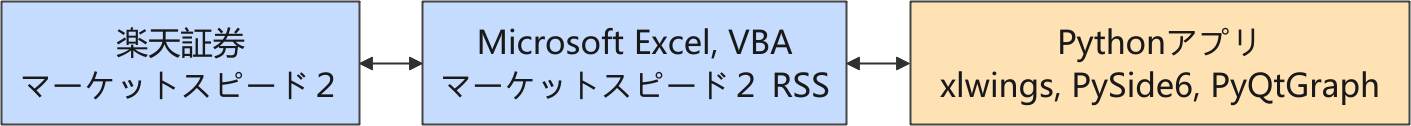
0 件のコメント:
コメントを投稿