楽天証券の口座でデイトレの自動売買に挑戦しようと Windows / Excel 上で利用できる マーケットスピード II RSS を活用して Python であれこれ取り組んでいます。この「自動売買への道」のトピックでは、プログラミングの話題にも踏み込んで、日々の活動をまとめていきます。
デイトレ用自作アプリ
以下は株価に関連する情報の流れを示しています。
楽天証券では、Python からネットワーク越しに直接取引できるような API が提供されていないので、マーケットスピード II RSS を介して取引をする構成を取っています。
取引シミュレーション
強化学習モデルのチューニング作業の優先順位を下げ、しばらくはテクニカル指標のシグナルで取引するアプローチを前面に出しています。
制約条件
現在シミュレーションで設定している制約は下記のとおりです。
- 売買条件
- ポジションを解消してから次の売買をする(ナンピン禁止)。
- 取引回数
- 上限を 100 回に制限
- 約定条件
- スリッページなし
売買判断のための指標
現在利用している指標は下記のとおりです。
- 2つの移動平均 MA1 と MA2
- クロスサインで売買(ナンピン売買禁止)
- 移動範囲 Moving Range, MR
- ボラティリティを判定する指標、しきい値以下の時はフラグを立ててエントリしない。
- PERIOD_MR = 30
- THRESHOLD_MR = 7
- ロスカット
- しきい値以下になったらフラグを立てて建玉を返済、損切り。
- 利確
- 含み益と含み益最大値との比較で建玉を返済、利確する簡単なロジックを導入。
実験計画
仮決め(上記)で利用してきた指標(因子)について、水準を振って、より良さげな条件の組み合わせを探索しています。
| 目 的 | PERIOD_MA_1 と PERIOD_MA_2 の水準を振って収益を最大化する組み合わせを探索する。 | ||||||
|---|---|---|---|---|---|---|---|
| データ | 楽天証券マーケットスピード2 RSS から取得した過去のティックデータ(銘柄コード 7011) | ||||||
| 実験因子 | 実験水準 | 説 明 | |||||
| PERIOD_MA_1 | sec | 50 | 70 | 90 | 110 | 130 | クロスシグナル判定用移動平均 MA1 の period |
| PERIOD_MA_2 | sec | 200 | 400 | 600 | 800 | 1000 | クロスシグナル判定用移動平均 MA2 の period |
| 評価特性 | 説 明 | ||||||
| 収益 (total) | 円 / 株 | 売買シミュレーションで、2 つの移動平均のクロスシグナルに従った収益。 | |||||
| 取引回数 (trade) | 回 | 【参考値】システム側でナンピン売買を禁止し、取引回数の上限を 100 回に設定。 | |||||
| 実験計画 | 説 明 | ||||||
| Full Factorial Design (完全実施要因計画) |
2 因子 5 水準の組み合わせ全て、すなわち 52 = 25 通りの条件。 この組み合わせを過去のティックデータファイルの数だけ、収益シュミレーションを繰り返します。 |
||||||
分析結果
実験データの分析方法が固まってきたので、今回は分析に使用した Python コード(Jupyter Lab 上)を併記しました。
関連ライブラリのインポート
まず、分析に必要なライブラリを一括してインポートします。
import datetime import os import matplotlib.font_manager as fm import matplotlib.pyplot as plt import matplotlib.ticker as ticker import numpy as np import pandas as pd import seaborn as sns import statsmodels.api as sm import statsmodels.formula.api as smf from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata from sklearn.preprocessing import StandardScaler from statsmodels.formula.api import ols
Matplotlib のフォント設定(オプション)
プロットには特定のフォントを使用したいので、最初に設定しています。
FONT_PATH = "../fonts/RictyDiminished-Regular.ttf" fm.fontManager.addfont(FONT_PATH) # FontPropertiesオブジェクト生成(名前の取得のため) font_prop = fm.FontProperties(fname=FONT_PATH) font_prop.get_name() plt.rcParams["font.family"] = font_prop.get_name()
シミュレーション済みのデータをロード
過去のティックデータごとに、DOE 条件でシミュレーションしたデータを読み込んで連結します。読み込むデータは、過去の取引日の付いた csv ファイルで、対象銘柄の当日のティックデータで、実験条件全てをシミュレーションした結果が保存されています。
name_doe = "doe-3"
name_code = "7011"
date_str = str(datetime.datetime.now().date()) # 保存ファイル目に付与する本日の日付
# データ読み込み
path_dir = os.path.join("..", "output", name_doe, name_code)
list_file = sorted(os.listdir(path_dir))
print(list_file)
list_df = list()
for file in list_file:
path = os.path.join(path_dir, file)
list_df.append(pd.read_csv(path))
n_tick = len(list_df)
print(f"\n# of tick files : {n_tick}")
df = pd.concat(list_df)
df.reset_index(inplace=True, drop=True)
df.to_csv("doe_results.csv", index=False)
['ticks_20250819.csv', 'ticks_20250820.csv', 'ticks_20250821.csv', 'ticks_20250822.csv', 'ticks_20250825.csv', 'ticks_20250826.csv', 'ticks_20250827.csv', 'ticks_20250828.csv', 'ticks_20250829.csv', 'ticks_20250901.csv', 'ticks_20250902.csv', 'ticks_20250903.csv', 'ticks_20250904.csv', 'ticks_20250905.csv', 'ticks_20250908.csv', 'ticks_20250909.csv', 'ticks_20250910.csv', 'ticks_20250911.csv', 'ticks_20250912.csv', 'ticks_20250916.csv', 'ticks_20250917.csv', 'ticks_20250918.csv', 'ticks_20250919.csv', 'ticks_20250922.csv', 'ticks_20250924.csv', 'ticks_20250925.csv', 'ticks_20250926.csv', 'ticks_20250929.csv', 'ticks_20250930.csv', 'ticks_20251001.csv', 'ticks_20251002.csv', 'ticks_20251003.csv', 'ticks_20251006.csv', 'ticks_20251007.csv', 'ticks_20251008.csv', 'ticks_20251009.csv', 'ticks_20251010.csv', 'ticks_20251014.csv', 'ticks_20251015.csv', 'ticks_20251016.csv', 'ticks_20251017.csv', 'ticks_20251020.csv', 'ticks_20251021.csv', 'ticks_20251022.csv', 'ticks_20251023.csv', 'ticks_20251024.csv', 'ticks_20251027.csv', 'ticks_20251028.csv', 'ticks_20251029.csv', 'ticks_20251030.csv', 'ticks_20251031.csv', 'ticks_20251104.csv', 'ticks_20251105.csv', 'ticks_20251106.csv', 'ticks_20251107.csv', 'ticks_20251110.csv', 'ticks_20251111.csv', 'ticks_20251112.csv', 'ticks_20251113.csv', 'ticks_20251114.csv', 'ticks_20251117.csv', 'ticks_20251118.csv', 'ticks_20251119.csv', 'ticks_20251120.csv', 'ticks_20251121.csv', 'ticks_20251125.csv', 'ticks_20251126.csv', 'ticks_20251127.csv', 'ticks_20251128.csv', 'ticks_20251201.csv', 'ticks_20251202.csv', 'ticks_20251203.csv', 'ticks_20251204.csv', 'ticks_20251205.csv']
# of tick files : 74
データの集計
今までは上記の連結したデータをそのまま分析していましたが、今回から集計したデータに対して分析するようにしました。
ティックデータ毎の収益 (total) の累計こそが重要なのですが、そうするとデータを殖やす度に値が変わることになってしまいます。そのため、便宜上、条件ごとの total の平均値を集計して分析をすることにしました。これをサマリデータと呼ぶことにします。
factor_cols = ["PERIOD_MA_1", "PERIOD_MA_2"]
response_cols = ["trade", "total"]
# 因子ごとに応答の平均を集計(サマリデータ)
df_summary = df.groupby(factor_cols)[response_cols].mean().reset_index()
print(df_summary)
# HTML 形式で出力
styled = df_summary.style.format(
{"trade": "{:.1f}", "total": "{:.2f}"}
).set_table_styles(
[
{"selector": "td", "props": "text-align: right;"},
]
)
html = styled.to_html()
with open("summary.html", "w", encoding="utf-8") as f:
f.write(html)
PERIOD_MA_1 PERIOD_MA_2 trade total
0 50 200 27.081081 -1.324324
1 50 400 18.945946 3.527027
2 50 600 15.108108 8.783784
3 50 800 13.891892 8.243243
4 50 1000 12.189189 4.635135
5 70 200 24.702703 1.216216
6 70 400 17.027027 4.378378
7 70 600 14.621622 8.689189
8 70 800 13.054054 7.824324
9 70 1000 12.054054 0.500000
10 90 200 22.567568 0.864865
11 90 400 14.756757 2.337838
12 90 600 12.108108 8.364865
13 90 800 10.918919 5.189189
14 90 1000 10.324324 1.770270
15 110 200 21.486486 -2.527027
16 110 400 12.918919 6.621622
17 110 600 11.000000 7.229730
18 110 800 9.918919 10.243243
19 110 1000 9.000000 6.256757
20 130 200 20.891892 1.594595
21 130 400 11.864865 6.229730
22 130 600 10.648649 8.540541
23 130 800 8.918919 8.662162
24 130 1000 8.675676 5.824324
HTML のテーブル形式でファイル (summary.html) へ出力をしており、CSS で修飾して本ブログで利用できるようにしています。
| PERIOD_MA_1 | PERIOD_MA_2 | trade | total | |
|---|---|---|---|---|
| 0 | 50 | 200 | 27.1 | -1.32 |
| 1 | 50 | 400 | 18.9 | 3.53 |
| 2 | 50 | 600 | 15.1 | 8.78 |
| 3 | 50 | 800 | 13.9 | 8.24 |
| 4 | 50 | 1000 | 12.2 | 4.64 |
| 5 | 70 | 200 | 24.7 | 1.22 |
| 6 | 70 | 400 | 17.0 | 4.38 |
| 7 | 70 | 600 | 14.6 | 8.69 |
| 8 | 70 | 800 | 13.1 | 7.82 |
| 9 | 70 | 1000 | 12.1 | 0.50 |
| 10 | 90 | 200 | 22.6 | 0.86 |
| 11 | 90 | 400 | 14.8 | 2.34 |
| 12 | 90 | 600 | 12.1 | 8.36 |
| 13 | 90 | 800 | 10.9 | 5.19 |
| 14 | 90 | 1000 | 10.3 | 1.77 |
| 15 | 110 | 200 | 21.5 | -2.53 |
| 16 | 110 | 400 | 12.9 | 6.62 |
| 17 | 110 | 600 | 11.0 | 7.23 |
| 18 | 110 | 800 | 9.9 | 10.24 |
| 19 | 110 | 1000 | 9.0 | 6.26 |
| 20 | 130 | 200 | 20.9 | 1.59 |
| 21 | 130 | 400 | 11.9 | 6.23 |
| 22 | 130 | 600 | 10.6 | 8.54 |
| 23 | 130 | 800 | 8.9 | 8.66 |
| 24 | 130 | 1000 | 8.7 | 5.82 |
分散分析 (ANOVA)
サマリデータに対して、主因子と交互作用について分散分析をしました。
# オリジナルのサマリデータをコピーして利用
df_anova = df_summary.copy()
# 因子列と応答変数
factor_cols = ["PERIOD_MA_1", "PERIOD_MA_2"]
X = df_anova[factor_cols]
y = df_anova["total"]
# 標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled_df = pd.DataFrame(X_scaled, columns=factor_cols)
# 標準化した因子を df_anova に置き換え
for col in factor_cols:
df_anova[col] = X_scaled_df[col]
# 二次交互作用まで含めるモデル
formula = "total ~ PERIOD_MA_1 + PERIOD_MA_2 + PERIOD_MA_1:PERIOD_MA_2"
model_2way = ols(formula, data=df_anova).fit()
# ANOVAテーブル
anova_table = sm.stats.anova_lm(model_2way, typ=2)
print("=== ANOVA (up to 2-way interactions) ===")
print(anova_table)
=== ANOVA (up to 2-way interactions) ===
sum_sq df F PR(>F)
PERIOD_MA_1 7.364500 1.0 0.662830 0.424699
PERIOD_MA_2 61.365234 1.0 5.523083 0.028621
PERIOD_MA_1:PERIOD_MA_2 0.591236 1.0 0.053213 0.819796
Residual 233.324363 21.0 NaN NaN
PERIOD_MA_2(長期移動平均)にやや有意性が認められますが強くはありません。
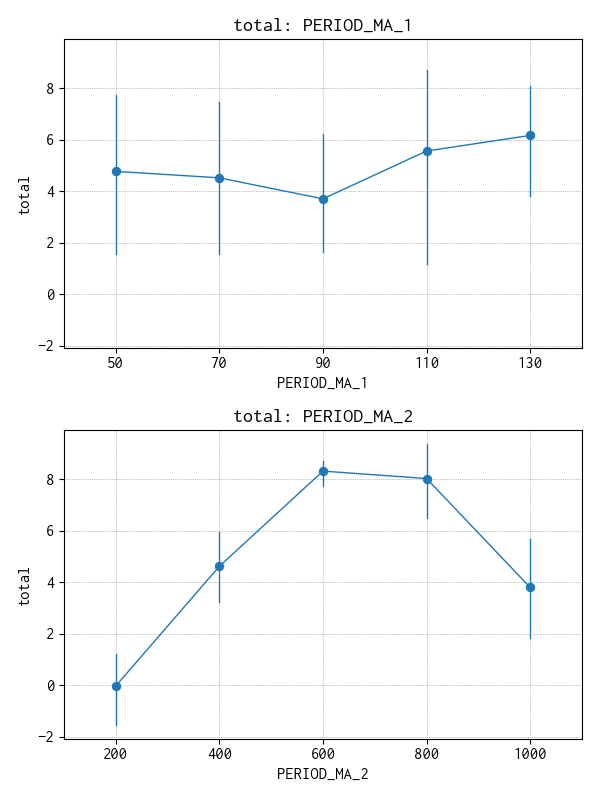
主効果
一応、主効果をプロットしました。
# === 各因子の平均効果を可視化 ===
list_col = ["PERIOD_MA_1", "PERIOD_MA_2"]
target = "total"
output = os.path.join(
"..", "output", name_doe, f"{name_code}_doe_effects_main_{target}_{date_str}.png"
)
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(len(list_col), 1, figsize=(6, 4 * len(list_col)))
y_min_global = 1e7
y_max_global = -1e7
for i, col in enumerate(list_col):
sns.pointplot(
x=col,
y=target,
data=df_summary,
markersize=6,
linewidth=1,
errorbar="ci",
ax=ax[i],
)
ax[i].grid(True, color="gray", linestyle="dotted", linewidth=0.5)
ax[i].set_title(f"{target}: {col}")
y_min, y_max = ax[i].get_ylim()
if y_min < y_min_global:
y_min_global = y_min
if y_max_global < y_max:
y_max_global = y_max
for i in range(len(list_col)):
ax[i].set_ylim(y_min_global, y_max_global)
plt.tight_layout()
plt.savefig(output)
plt.show()
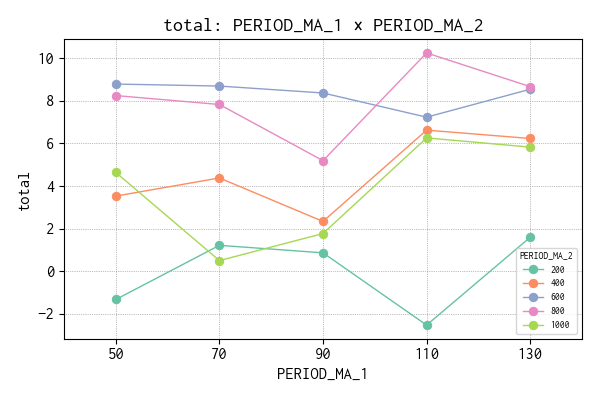
交互作用効果
交互作用も同様にプロットしました。
target = "total"
output = os.path.join(
"..",
"output",
name_doe,
f"{name_code}_doe_effects_interaction_{target}_{date_str}.png",
)
"""
pairs = [
("PERIOD_MA_1", "PERIOD_MA_2"),
]
a, b = pairs[0]
"""
a = "PERIOD_MA_1"
b = "PERIOD_MA_2"
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(1, 1, figsize=(6, 4))
sns.pointplot(
x=a,
y=target,
hue=b,
data=df_summary,
markersize=6,
linewidth=1,
errorbar=None,
palette="Set2",
ax=ax,
)
ax.set_title(f"{target}: {a} × {b}")
ax.set_xlabel(a)
ax.set_ylabel(target)
ax.grid(True, color="gray", linestyle="dotted", linewidth=0.5)
# 凡例のタイトル
lg = ax.legend(fontsize=7)
lg.set_title(b, prop={"size": 7})
plt.tight_layout()
plt.savefig(output)
plt.show()
交互作用のチャートによると、PERIOD_MA_2 = 300 の水準は今後外しても良さそうです。
重回帰分析 (MULREG)
実験因子の二次の多項式モデルを定義して、サマリデータに対して重回帰分析をしました。
# ---------------------------------------------------------
# 2. RSM 用の二次モデルを構築
# total ~ PERIOD_MA_1 + PERIOD_MA_2 + 交互作用 + 二乗項
# ---------------------------------------------------------
formula = """
total ~ PERIOD_MA_1 + PERIOD_MA_2
+ I(PERIOD_MA_1**2) + I(PERIOD_MA_2**2)
+ PERIOD_MA_1:PERIOD_MA_2
"""
model = smf.ols(formula, data=df_summary).fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: total R-squared: 0.811
Model: OLS Adj. R-squared: 0.761
Method: Least Squares F-statistic: 16.31
Date: Sat, 06 Dec 2025 Prob (F-statistic): 2.67e-06
Time: 11:38:10 Log-Likelihood: -45.815
No. Observations: 25 AIC: 103.6
Df Residuals: 19 BIC: 110.9
Df Model: 5
Covariance Type: nonrobust
===========================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------
Intercept -4.2290 4.878 -0.867 0.397 -14.438 5.980
PERIOD_MA_1 -0.1334 0.098 -1.367 0.188 -0.338 0.071
PERIOD_MA_2 0.0505 0.007 6.777 0.000 0.035 0.066
I(PERIOD_MA_1 ** 2) 0.0008 0.001 1.512 0.147 -0.000 0.002
I(PERIOD_MA_2 ** 2) -3.888e-05 5.18e-06 -7.500 0.000 -4.97e-05 -2.8e-05
PERIOD_MA_1:PERIOD_MA_2 1.922e-05 4.34e-05 0.443 0.663 -7.15e-05 0.000
==============================================================================
Omnibus: 4.069 Durbin-Watson: 2.127
Prob(Omnibus): 0.131 Jarque-Bera (JB): 1.590
Skew: -0.164 Prob(JB): 0.452
Kurtosis: 1.809 Cond. No. 7.91e+06
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 7.91e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
フィッティング (Adj. R-squared) はそこそこあります。Cond. No. がやたら大きく、多重共線性が強く出ていますが、Full Factorial Design のせいだと考えて、ここは許容することにします。
もともと Full Factorial Design にした理由は、線形モデルで近似できるかどうかわからない実験対象に対して、直交性を重視した(= 条件に抜けがある)実験計画を立てるより、できるだけ条件に抜けがない(= Full Factorial)実験計画を採用して、最適値近辺のパフォーマンスを実験値で確認できるようにしたかったからなのです。
分散分析のときと有意性の傾向は似ていて、PERIOD_MA_2(長周期移動平均)は有意ですが、交互作用効果 PERIOD_MA_1 x PERIOD_MA_2 は有意ではありません。
応答曲面 (RSM)
重回帰分析で作成したモデル model を利用して応答曲面を三次元的にプロットして鳥瞰してみます。
# ---------------------------------------------------------
# 3. 予測用のグリッドを作成して応答曲面を描く準備
# ---------------------------------------------------------
ma1_range = np.linspace(
df_summary["PERIOD_MA_1"].min(), df_summary["PERIOD_MA_1"].max(), 100
)
ma2_range = np.linspace(
df_summary["PERIOD_MA_2"].min(), df_summary["PERIOD_MA_2"].max(), 100
)
MA1, MA2 = np.meshgrid(ma1_range, ma2_range)
grid = pd.DataFrame({"PERIOD_MA_1": MA1.ravel(), "PERIOD_MA_2": MA2.ravel()})
grid["pred"] = model.predict(grid)
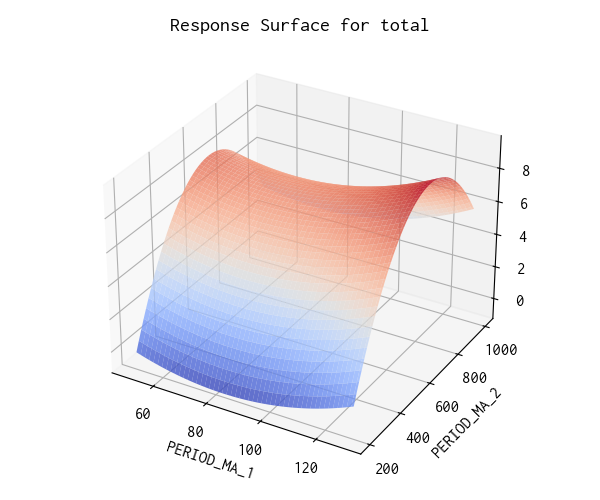
3D 応答曲面
# ---------------------------------------------------------
# 4. 3D 応答曲面プロット(matplotlib)
# ---------------------------------------------------------
plt.rcParams["font.size"] = 12
fig = plt.figure(figsize=(6, 5))
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(
MA1, MA2, grid["pred"].values.reshape(MA1.shape), cmap="coolwarm", alpha=0.8
)
ax.set_xlabel("PERIOD_MA_1")
ax.set_ylabel("PERIOD_MA_2")
ax.set_title("Response Surface for total")
output = os.path.join(
"..", "output", name_doe, f"{name_code}_rsm_surface_1_{target}_{date_str}.png"
)
plt.tight_layout()
plt.savefig(output)
plt.show()
PERIOD_MA_2 = 600 あたりに沿って鞍状に収益が極大なっています。多少の差異はありますが短周期の PERIOD_MA_1 との交互作用があまりないのは意外です。
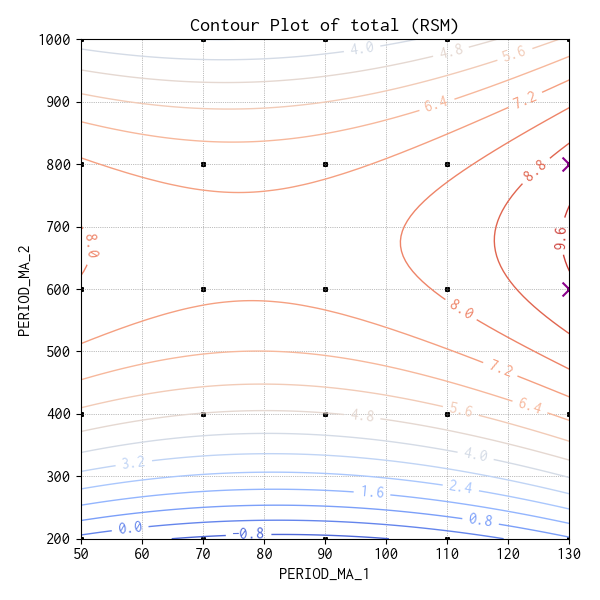
等高線図
3D 応答曲面は全体的傾向を視覚的に確認するのにはインパクトがありますが、パフォーマンス(この場合は収益)の数値を確認するためには等高線図の方が具体的です。
# ---------------------------------------------------------
# 5. グラデーション付き等高線(塗りつぶしなし)
# ---------------------------------------------------------
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(6, 6))
Z = grid["pred"].values.reshape(MA1.shape)
# 等高線(線にグラデーション)
cont = ax.contour(MA1, MA2, Z, levels=15, cmap="coolwarm", linewidths=1)
# 数値ラベル
ax.clabel(cont, inline=True, fontsize=12, fmt="%.1f")
ax.set_xlabel("PERIOD_MA_1")
ax.set_ylabel("PERIOD_MA_2")
ax.set_title("Contour Plot of total (RSM)")
ax.grid(True, color="gray", linestyle="dotted", linewidth=0.5)
# 実験点を黒点で追加
ax.scatter(
df["PERIOD_MA_1"], df["PERIOD_MA_2"], color="black", s=5, alpha=0.9 # 点の大きさ
)
# 最適点
ax.scatter([130, 130], [600, 800], color="darkmagenta", s=100, marker="x")
output = os.path.join(
"..", "output", name_doe, f"{name_code}_rsm_contour_1_{target}_{date_str}.png"
)
plt.tight_layout()
plt.savefig(output)
plt.show()
等高線図で確認すると、PERIOD_MA_2 = 600 ~ 700 あたりで収益が高くなっています。等高線が正しければ、PERIOD_MA_1 = 130 より大きい条件、あるいは PERIOD_MA_1 = 50 より小さい方向に、収益を最大化できる条件があることを示唆しています。
等高線図右側に × を付けた実験条件では、最大と言えないまでも確かに高い平均収益 (total) になっています。
| PERIOD_MA_1 | PERIOD_MA_2 | trade | total | |
|---|---|---|---|---|
| 22 | 130 | 600 | 10.6 | 8.54 |
| 23 | 130 | 800 | 8.9 | 8.66 |
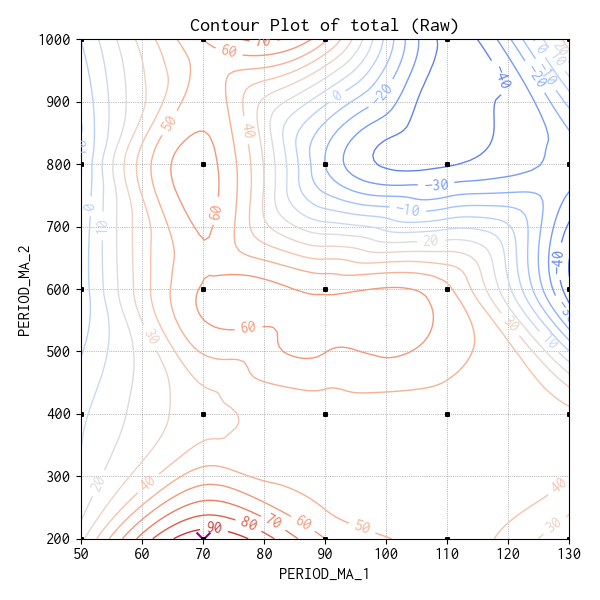
生データによる等高線図
念の為、サマリデータの平均収益を利用せず、25(条件) × 74(ティックデータ) の生データから作成した等高線図も作ってみました。
# ---------------------------------------------------------
# 6. グリッドを作成して実データを補完した曲面を描く準備
# ---------------------------------------------------------
col_x = "PERIOD_MA_1"
col_y = "PERIOD_MA_2"
col_z = "total"
x = df[col_x]
y = df[col_y]
z = df[col_z]
# グリッド作成
xi = np.linspace(x.min(), x.max(), 100)
yi = np.linspace(y.min(), y.max(), 100)
# 補間
Xi, Yi = np.meshgrid(xi, yi)
Zi = griddata((x, y), z, (Xi, Yi), method="cubic")
# ---------------------------------------------------------
# 5. グラデーション付き等高線(塗りつぶしなし)
# ---------------------------------------------------------
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(6, 6))
# Contour Map
cont = ax.contour(Xi, Yi, Zi, levels=15, cmap="coolwarm", linewidths=1)
ax.clabel(cont, inline=True, fontsize=12)
ax.set_xlabel(col_x)
ax.set_ylabel(col_y)
ax.set_title("Contour Plot of total (Raw)")
ax.grid(True, color="gray", linestyle="dotted", linewidth=0.5)
# 実験点を黒丸で追加
ax.scatter(x, y, color="black", s=5, zorder=3)
# 最適点
ax.scatter([70], [200], color="darkmagenta", s=100, marker="x")
output = os.path.join(
"..", "output", name_doe, f"{name_code}_raw_contour_1_{target}_{date_str}.png"
)
plt.tight_layout()
plt.savefig(output)
plt.show()
等高線図 (70, 200) あたりが最も高い収益の領域になっています。こちらもチャートの端に極大点があるのが気に入りません。サマリデータを確認してみたところ、この条件の平均収益はプラスではあるものの決して高い値ではありませんでした。
| PERIOD_MA_1 | PERIOD_MA_2 | trade | total | |
|---|---|---|---|---|
| 5 | 70 | 200 | 24.7 | 1.22 |
生データから補完して等高線図を作成しているからと言っても、必ずしも妥当な傾向を示しているとは限らないようです。まあ、同じ条件でもティックデータが違えばパフォーマンスも変わるので仕方がありません。今まではちょっと信用しすぎたようです。
次のステップ
分析結果にしたがって、PERIOD_MA_1 をさらに右側(大きくする方向)にずらし水準幅を広げ、PERIOD_MA_2 は水準幅を縮めてみることにしました。これで、シミュレーション評価をする予定です。
| 実験因子 | 実験水準 | |||||
|---|---|---|---|---|---|---|
| PERIOD_MA_1 | sec | 60 | 90 | 120 | 150 | 180 |
| PERIOD_MA_2 | sec | 500 | 600 | 700 | 800 | 900 |
参考サイト
- マーケットスピード II RSS | 楽天証券のトレーディングツール
- マーケットスピード II RSS 関数マニュアル
- 注文 | マーケットスピード II RSS オンラインヘルプ | 楽天証券のトレーディングツール
- Gymnasium Documentation
- Stable-Baselines3 Docs - Reliable Reinforcement Learning Implementations
- Maskable PPO — Stable Baselines3 - documentation
- PyTorch documentation
- PythonでGUIを設計 | Qtの公式Pythonバインディング
- Python in Excel alternative: Open. Self-hosted. No limits.
- Book - xlwings Documentation


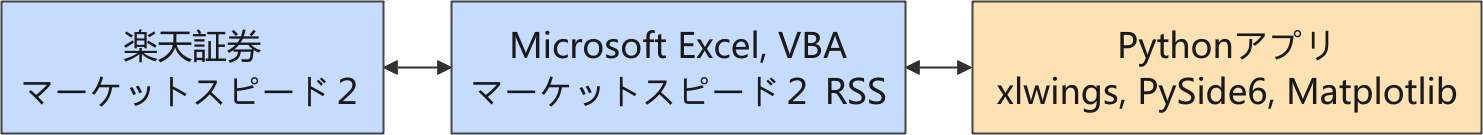
0 件のコメント:
コメントを投稿