楽天証券の口座でデイトレの自動売買に挑戦しようと Windows / Excel 上で利用できる マーケットスピード II RSS を活用して Python であれこれ取り組んでいます。この「自動売買への道」のトピックでは、プログラミングの話題にも踏み込んで、日々の活動をまとめていきます。
今日の日経平均株価
| 現在値 | 49,303.45 | +0.17 | 0.00% | 15:30 | |
|---|---|---|---|---|---|
| 前日終値 | 49,303.28 | 12/01 | 高値 | 49,636.79 | 10:16 |
| 始値 | 49,494.58 | 09:00 | 安値 | 49,243.55 | 15:22 |
※ 右の 15 分足チャートは Yahoo! Finance のデータを yfinance で取得して作成しました。
【関連ニュース】
- エヌビディア株、泣く泣く売ったとソフトバンクG孫社長-資金調達で - Bloomberg [2025-12-01]
- 米エヌビディア、半導体設計ソフトのシノプシスに20億ドル出資 | ロイター [2025-12-02]
- 米国株式市場=反落、ダウ427ドル安 米国債利回り上昇が重し | ロイター [2025-12-02]
- 中国DeepSeek、次世代AIに向け布石-最新の実験バージョン発表 - Bloomberg [2025-12-02]
- 東京株式市場・大引け=横ばい、前日安から反発後に失速 月初の需給売り観測も | ロイター [2025-12-02]
デイトレ用自作アプリ
以下は株価に関連する情報の流れを示しています。
楽天証券では、Python からネットワーク越しに直接取引できるような API が提供されていないので、マーケットスピード II RSS を介して取引をする構成を取っています。
取引シミュレーション
強化学習モデルのチューニング作業の優先順位を下げ、しばらくはテクニカル指標のシグナルで取引するアプローチを前面に出しています。
現在利用している指標は下記のとおりです。
- 2つの移動平均 MA (n = 60 sec) と MA (n = 600 sec)
- クロスサインで売買(ナンピン売買禁止)
- 移動範囲 Moving Range, MR (n = 60 sec)
- ボラティリティを判定する指標、しきい値以下の時はフラグを立ててエントリしない。
- ロスカット
- しきい値以下になったらフラグを立てて建玉を返済、損切り。
- 利確
- 含み益と含み益最大値との比較で建玉を返済、利確する簡単なロジックを導入。
実験計画
仮決め(上記)で利用してきた指標(因子)について、水準を振って、より良さげな条件の組み合わせを探索しようとしています。実験因子として水準を振れるような機能をアプリに追加しました。
目的
仮決めで利用してきた指標(因子)の水準の前後で振った範囲内に最低条件が存在するかどうかを確認する。
実験範囲内に最適水準があれば、シミュレーションの使用するパラメータの水準を変更する。
実験範囲外に最適水準がありそうであれば、実験範囲をその方向に広げて最適な条件を探索する。
実験因子
上記のロスカットと利確条件も因子に加えたかったのですが、残念ながら納得できるやりかたに落ち着いていません。ひとまず、この 2 因子の機能はオフ(ロスカット、利確なし)にして実験評価をすることにしました。
- PERIOD_MA_1
- 移動平均 1 の period
- 水準 : 30, 60, 90 [sec]
- PERIOD_MA_2
- 移動平均 2 の period
- 水準 : 300, 600, 900 [sec]
- PERIOD_MR
- 移動範囲 の period
- 水準 : 15, 30, 45 [sec]
- THRESHOLD_MR
- エントリを禁止する移動範囲のしきい値
- 水準 : 1, 4, 7 [sec]
評価特性
- 1 株当りの収益
- [参考評価]100 回を上限としている取引回数
実験の組み合わせ
4 因子 3 水準の組み合わせ、34 = 81 通りの条件を、過去のティックデータ 70 日分全て (81 × 70 = 5670 run) に適用して、収益シミュレーションを実施しています。全ての run が完了するのは 12/3 の朝方になると見込んでいます。
準備(予行練習)
結果が出るまでの間、メインの PC で昨日算出した過去 3 日分 (11/27, 28, 12/1) のデータを使って JupyterLab 上で分析方法の検討をしました。
ライブラリのインポート
まず、必要なライブラリをまとめてインポートしておきます。
import os import matplotlib.font_manager as fm import matplotlib.pyplot as plt import matplotlib.ticker as ticker import numpy as np import pandas as pd import seaborn as sns import statsmodels.api as sm from scipy.interpolate import griddata from sklearn.linear_model import LassoCV from sklearn.metrics import r2_score from sklearn.pipeline import make_pipeline from sklearn.preprocessing import PolynomialFeatures, StandardScaler from statsmodels.formula.api import ols
Matplotlib の設定(オプション)
Matplotlib の設定をしておきます。好みのフォントを使いたいための設定なので、ここは省略可能です。
FONT_PATH = "../fonts/RictyDiminished-Regular.ttf" fm.fontManager.addfont(FONT_PATH) # FontPropertiesオブジェクト生成(名前の取得のため) font_prop = fm.FontProperties(fname=FONT_PATH) font_prop.get_name() plt.rcParams["font.family"] = font_prop.get_name() plt.rcParams["font.size"] = 14
CSV ファイルの読込
昨日j算出した 3 日分の csv ファイルを読み込みます。
# データ読み込み
file_csv = "../logs/result_20251201162005.csv"
file_body = os.path.splitext(os.path.basename(file_csv))[
0
] # プロットの保存用ファイル名
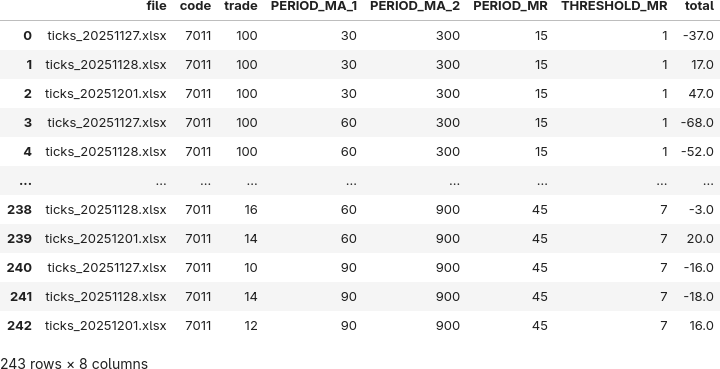
df = pd.read_csv(file_csv)
df
分散分析 (ANOVA)
最初は定番の分散分析です。ANOVA のモデルは、興味がある交互作用 PERIOD_MA_1 x PERIOD_MA_2 と PERIOD_MR x THRESHOLD_MR に絞ってます。
# オリジナルのデータフレームをコピーして利用
df_anova = df.copy()
# 因子をカテゴリ化
factor_cols = ["PERIOD_MA_1", "PERIOD_MA_2", "PERIOD_MR", "THRESHOLD_MR"]
for c in factor_cols:
df_anova[c] = df_anova[c].astype("category")
# ANOVA(注視交互作用のみ)
formula = "total ~ C(PERIOD_MA_1)*C(PERIOD_MA_2) + C(PERIOD_MR)*C(THRESHOLD_MR)"
model = ols(formula, data=df).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table)
sum_sq df F PR(>F)
C(PERIOD_MA_1) 304.617284 2.0 0.269555 7.639641e-01
C(PERIOD_MA_2) 21292.617284 2.0 18.841811 2.703069e-08
C(PERIOD_MR) 4732.518519 2.0 4.187800 1.637393e-02
C(THRESHOLD_MR) 39428.222222 2.0 34.889985 6.234240e-14
C(PERIOD_MA_1):C(PERIOD_MA_2) 743.876543 4.0 0.329128 8.582317e-01
C(PERIOD_MR):C(THRESHOLD_MR) 1484.444444 4.0 0.656792 6.226598e-01
Residual 127698.222222 226.0 NaN NaN
この結果では、主効果の一部は有意ですが、指定した交互作用は有意ではありませんでした。
- 有意な主効果
- PERIOD_MA_2(p ≈ 2.7e-08) → 長期移動平均期間は total に強く影響
- PERIOD_MR(p ≈ 0.016) → 移動範囲も影響あり
- THRESHOLD_MR(p ≈ 6.2e-14) → 閾値は非常に強い影響
- 有意でない主効果
- PERIOD_MA_1(p ≈ 0.76) → 短期移動平均期間は影響が弱い
- 交互作用(注視していた2つ)
- PERIOD_MA_1 × PERIOD_MA_2 → p ≈ 0.86(有意でない)
- PERIOD_MR × THRESHOLD_MR → p ≈ 0.62(有意でない)
過去 70 日分のデータの分析でどうなるか注目です。
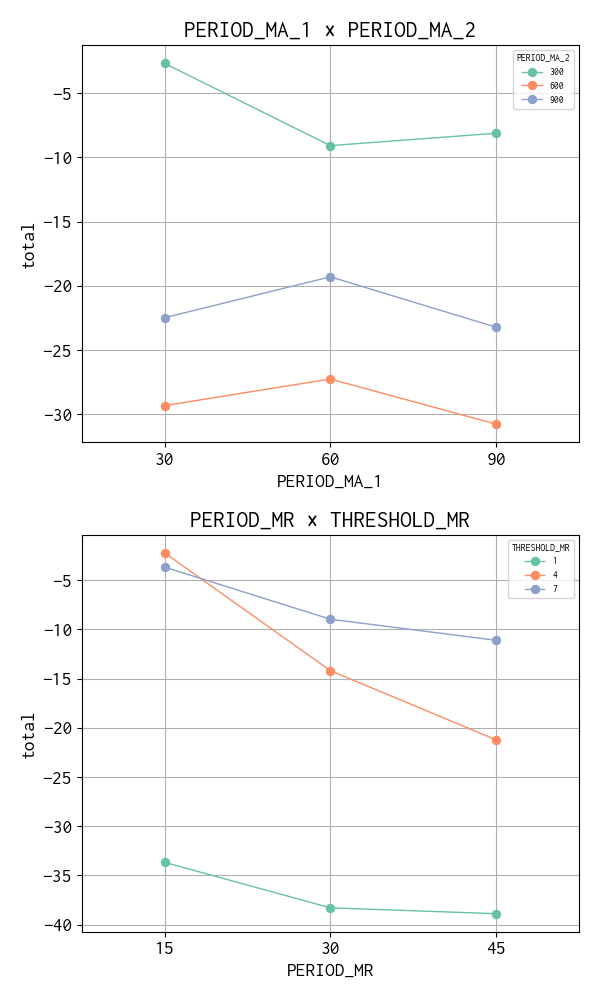
主効果+交互作用 プロット
主効果および交互作用の関係を視覚化します。
output = os.path.join("..", "logs", f"{file_body}_effects.png")
pairs = [
("PERIOD_MA_1", "PERIOD_MA_2"),
("PERIOD_MR", "THRESHOLD_MR"),
]
fig, axes = plt.subplots(2, 1, figsize=(6, 10))
for ax, (a, b) in zip(axes, pairs):
sns.pointplot(
x=a,
y="total",
hue=b,
data=df,
markersize=6,
linewidth=1,
errorbar=None,
palette="Set2",
ax=ax,
)
ax.set_title(f"{a} × {b}")
ax.set_xlabel(a)
ax.set_ylabel("total")
lg = ax.legend(fontsize=7)
lg.set_title(b, prop={"size": 7})
ax.grid()
plt.tight_layout()
plt.savefig(output)
plt.show()
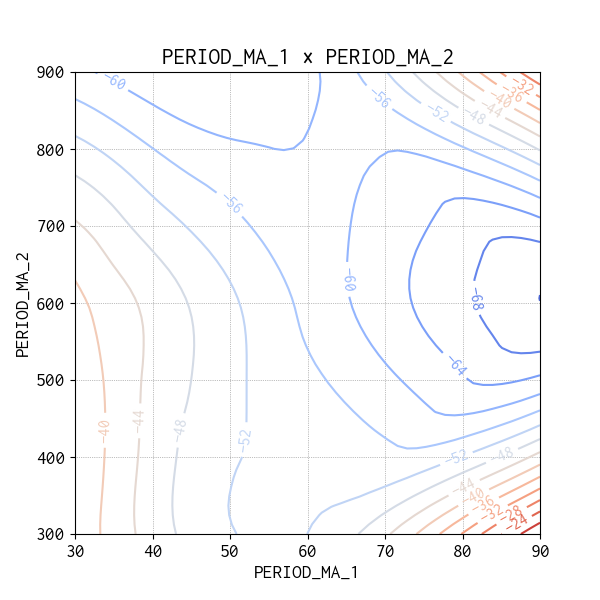
交互作用の等高線図
今回は水準の組み合わせ全て(Full Factorial Design)の売買シミュレーションを実施していますので、生データを使って Contour Map(等高線図)をプロットすることができます。分散分析の結果は有意ではありませんでしたが、興味ある因子間の交互作用を確認してみました。
def plot_contour(col_x: str, col_y: str, col_z: str, output: str):
x = df[col_x]
y = df[col_y]
z = df[col_z]
# グリッド作成
xi = np.linspace(x.min(), x.max(), 50)
yi = np.linspace(y.min(), y.max(), 50)
Xi, Yi = np.meshgrid(xi, yi)
# 補間
Zi = griddata((x, y), z, (Xi, Yi), method="cubic")
plt.figure(figsize=(6, 6))
cont = plt.contour(Xi, Yi, Zi, levels=15, cmap="coolwarm")
plt.clabel(cont, inline=True, fontsize=12)
plt.title(f"{col_x} × {col_y}")
plt.xlabel(col_x)
plt.ylabel(col_y)
plt.grid(True, color="gray", linestyle="dotted", linewidth=0.5)
plt.savefig(output)
plt.show()
# ===== 1. PERIOD_MA_1 × PERIOD_MA_2 =====
output = os.path.join("..", "logs", f"{file_body}_contour_1.png")
plot_contour("PERIOD_MA_1", "PERIOD_MA_2", "total", output)
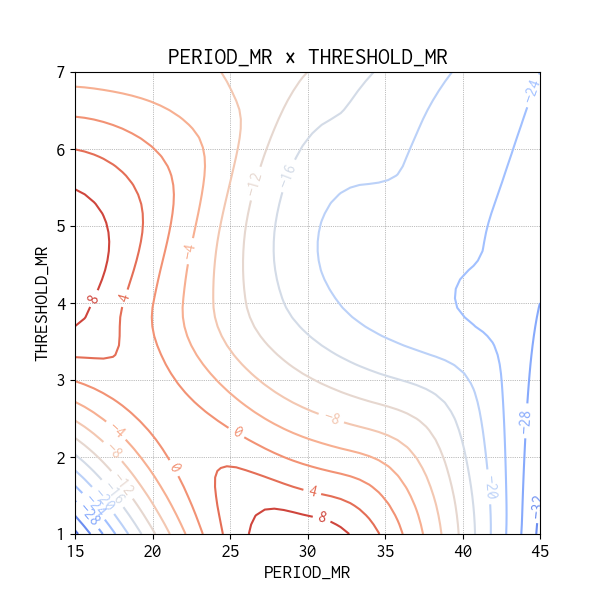
# ===== 2. PERIOD_MR × THRESHOLD_MR =====
output = os.path.join("..", "logs", f"{file_body}_contour_2.png")
plot_contour("PERIOD_MR", "THRESHOLD_MR", "total", output)
収益が高い方向は赤い等高線の方向になるので、3 日分のデータではどちらの等高線図をみても、今回の実験水準の範囲の外により最適な水準があることを示唆しています。
二次多項式と Lasso 回帰
分散分析の結果は、3 日分のデータだけとは言え、注目していた交互作用が有意ではない、という残念な結果になりましたが、別のアプローチをすると違った結果が出てきました。
分散分析では因子をカテゴリ化してしまうので、RSM(応答局面法)という重回帰分析のアプローチをしようと、二次多項式から有意でない因子を手作業でひとつひとつ確認していました。もっとスマートな方法がないか生成 AI (Microsoft Copilot) に確認したところ Lasso 回帰を教えてもらいました。
Lasso, Least Absolute Shrinkage and Selection Operator(ラッソ回帰)とは、線形回帰に「L1 正則化」を加えた手法で、不要な変数を自動的にゼロにして特徴選択を行える回帰モデルです。
機械学習で「Lasso 回帰」や「L1 正則化」は知っていたものの、見たことがあるという程度に過ぎず、利用したことがありませんでした。しかし、重回帰分析の多項式における変数選択を特徴量選択という名前に置き換えることによって、ありがたみが判りました。
生成 AI に提案してもらったコードで試してみました。
# 1. 因子を数値として扱う
factor_cols = ["PERIOD_MA_1", "PERIOD_MA_2", "PERIOD_MR", "THRESHOLD_MR"]
X = df[factor_cols]
y = df["total"]
# 2. 二次回帰+Lasso
poly = PolynomialFeatures(degree=2, include_bias=False)
lasso = LassoCV(cv=5, random_state=0)
model = make_pipeline(poly, lasso).fit(X, y)
# 3. サマリ統計
# 展開後の特徴量名を取得
feature_names = poly.get_feature_names_out(factor_cols)
# 係数を取り出し
coef = model.named_steps["lassocv"].coef_
# 結果をDataFrameにまとめる
summary = pd.DataFrame({"feature": feature_names, "coefficient": coef})
# 非ゼロ係数のみ表示
summary_nonzero = summary[summary["coefficient"] != 0]
print("=== Lassoによる選択結果(非ゼロ係数) ===")
print(summary_nonzero)
# モデル性能
y_pred = model.predict(X)
print("\nR^2:", r2_score(y, y_pred))
print("Best alpha (正則化パラメータ):", model.named_steps["lassocv"].alpha_)
=== Lassoによる選択結果(非ゼロ係数) ===
feature coefficient
5 PERIOD_MA_1 PERIOD_MA_2 -0.000103
8 PERIOD_MA_2^2 -0.000020
9 PERIOD_MA_2 PERIOD_MR -0.000620
10 PERIOD_MA_2 THRESHOLD_MR 0.007179
R^2: 0.256173893165923
Best alpha (正則化パラメータ): 1506.2962962962977
データをスケーリング(標準化)していないので、結果の係数の大きさをそのまま議論できませんが、残った因子には興味のあった因子の交互作用とは少し違いますが、交互作用の形で残っています。
参考サイト
- マーケットスピード II RSS | 楽天証券のトレーディングツール
- マーケットスピード II RSS 関数マニュアル
- 注文 | マーケットスピード II RSS オンラインヘルプ | 楽天証券のトレーディングツール
- Gymnasium Documentation
- Stable-Baselines3 Docs - Reliable Reinforcement Learning Implementations
- Maskable PPO — Stable Baselines3 - documentation
- PyTorch documentation
- PythonでGUIを設計 | Qtの公式Pythonバインディング
- Python in Excel alternative: Open. Self-hosted. No limits.
- Book - xlwings Documentation


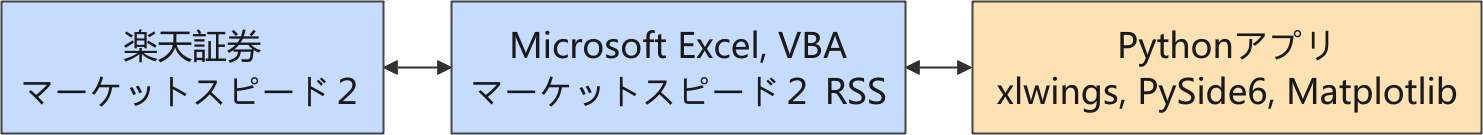
0 件のコメント:
コメントを投稿