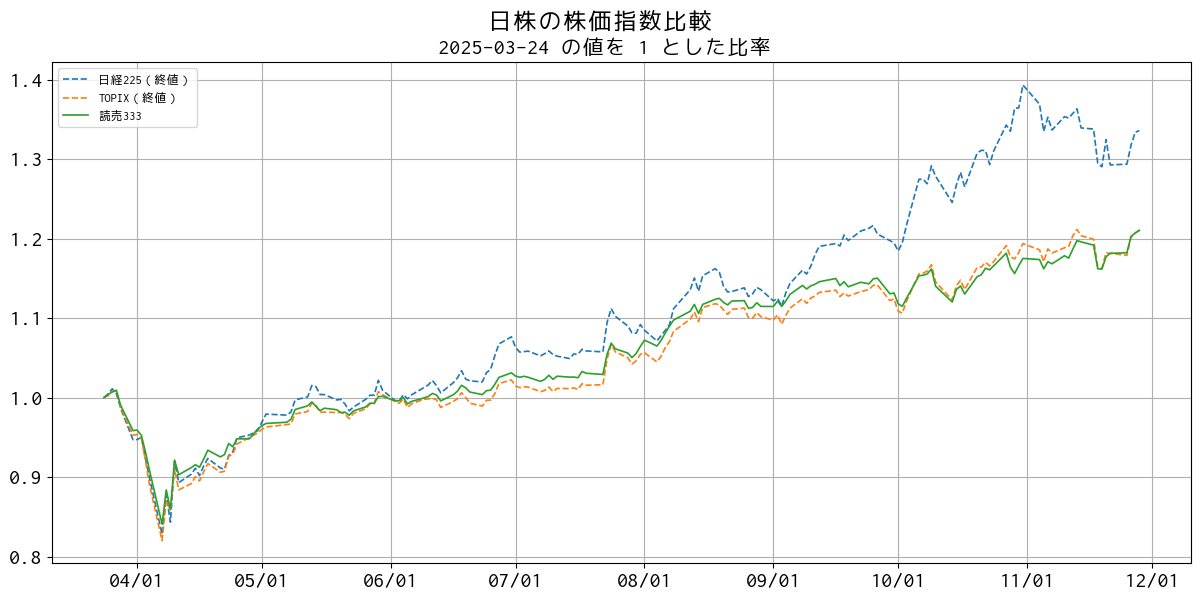
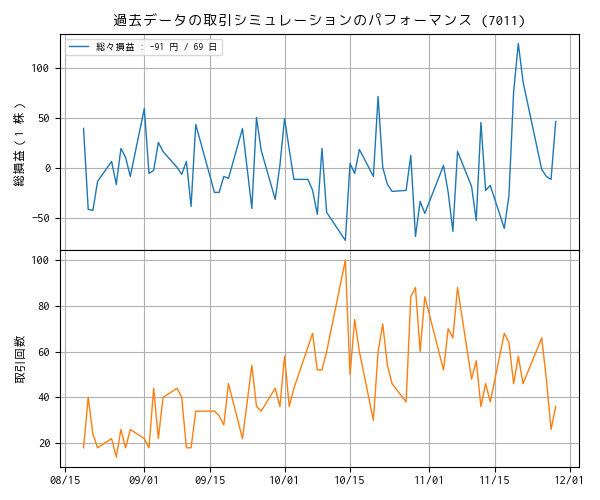
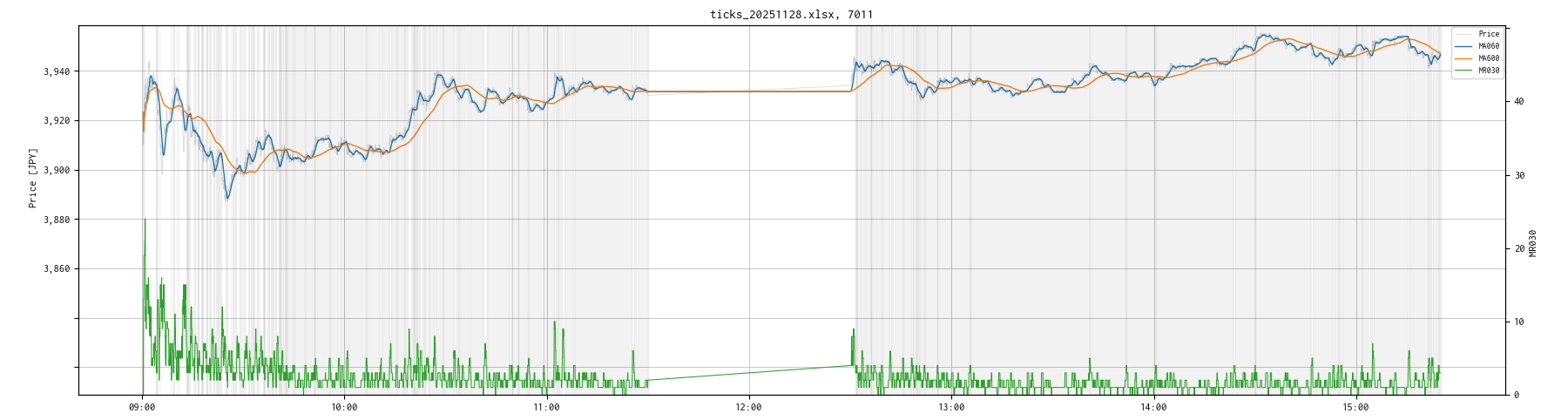
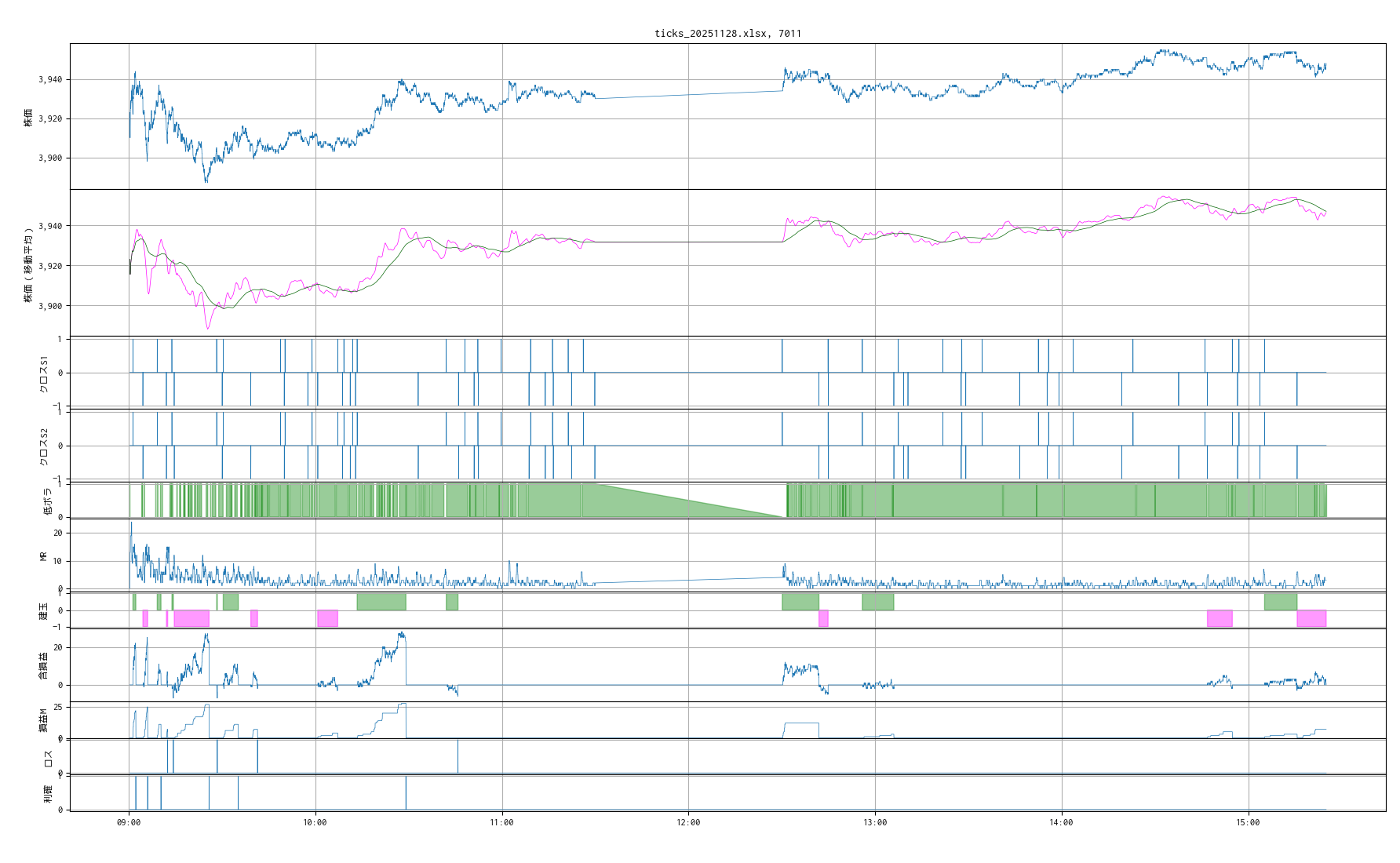
本ブログの過去記事 [1] に書いたように、正規分布に従っていないデータに対して平均値 average、標準偏差 σ を使用することはやめ、ロバスト統計量と呼ばれる median(中央値)と IQR(四分位範囲)を採用しています。
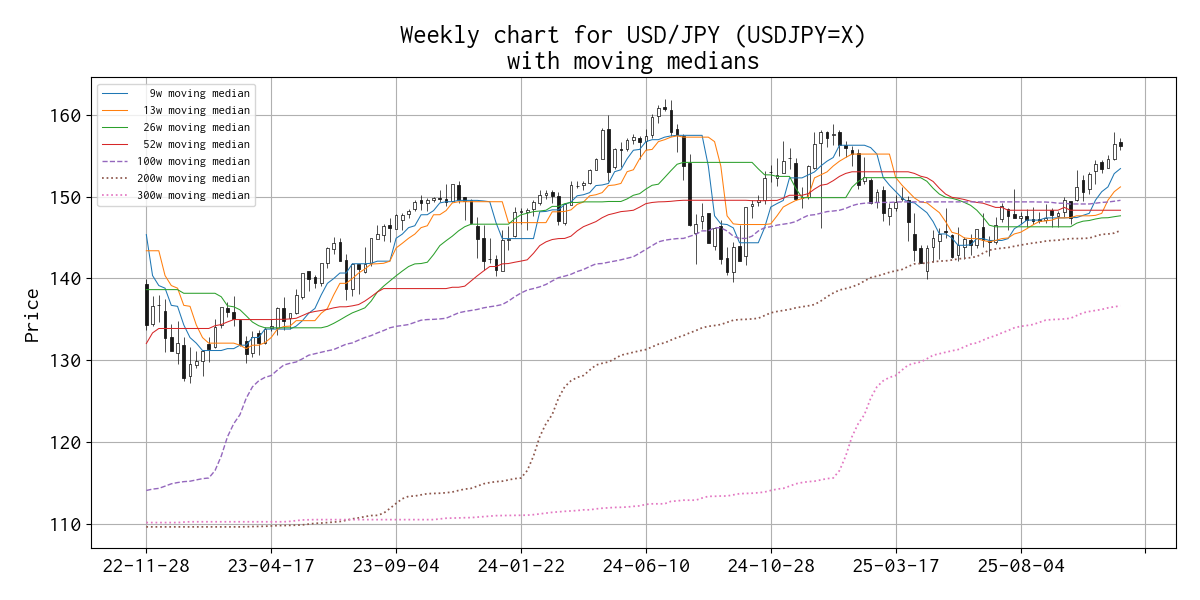
今週は 156.137 円で引け、先週に比べ -0.273 円差、 つまり円高になり、週足では陰線を形成しました。
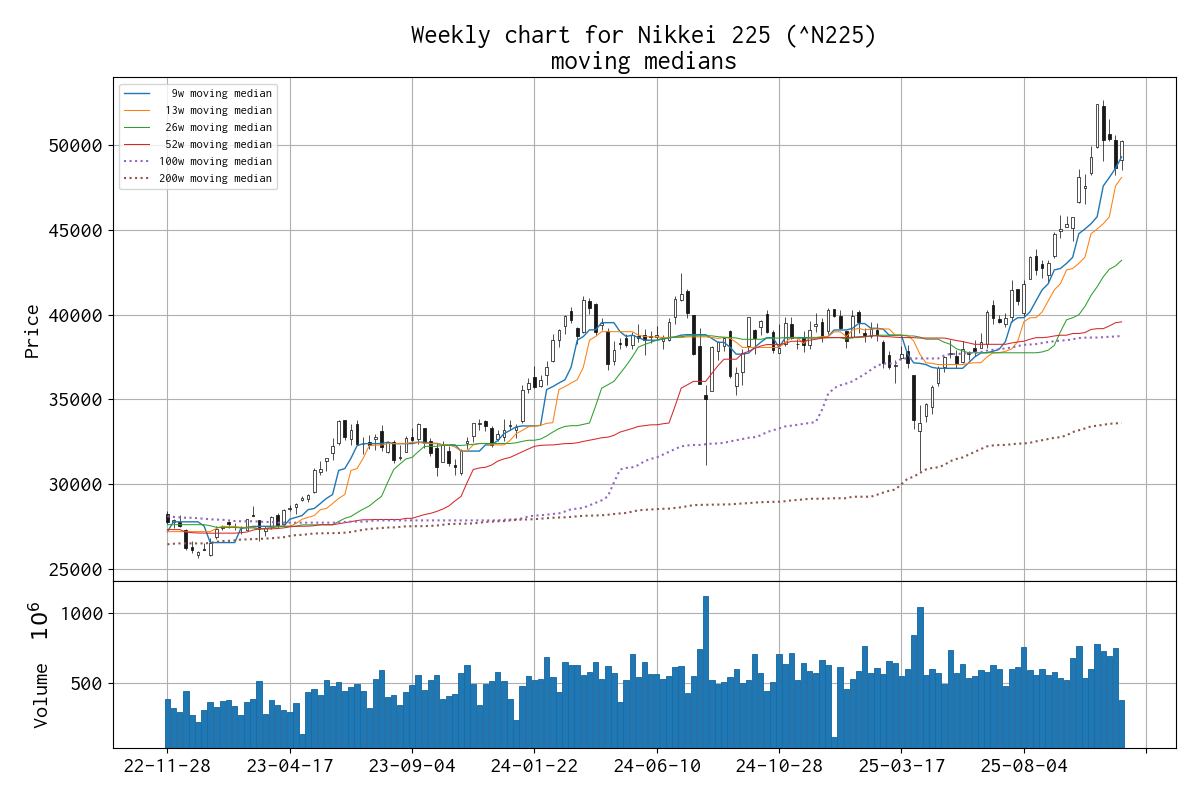
直近の移動メジアン線の値は、 9 週線 153.420 円、 13 週線 151.180 円、 26 週線 147.647 円、 52 週線 148.325 円(9 週連続)、 100 週線 149.538 円、 200 週線 145.847 円、 300 週線 136.640 円 でした。
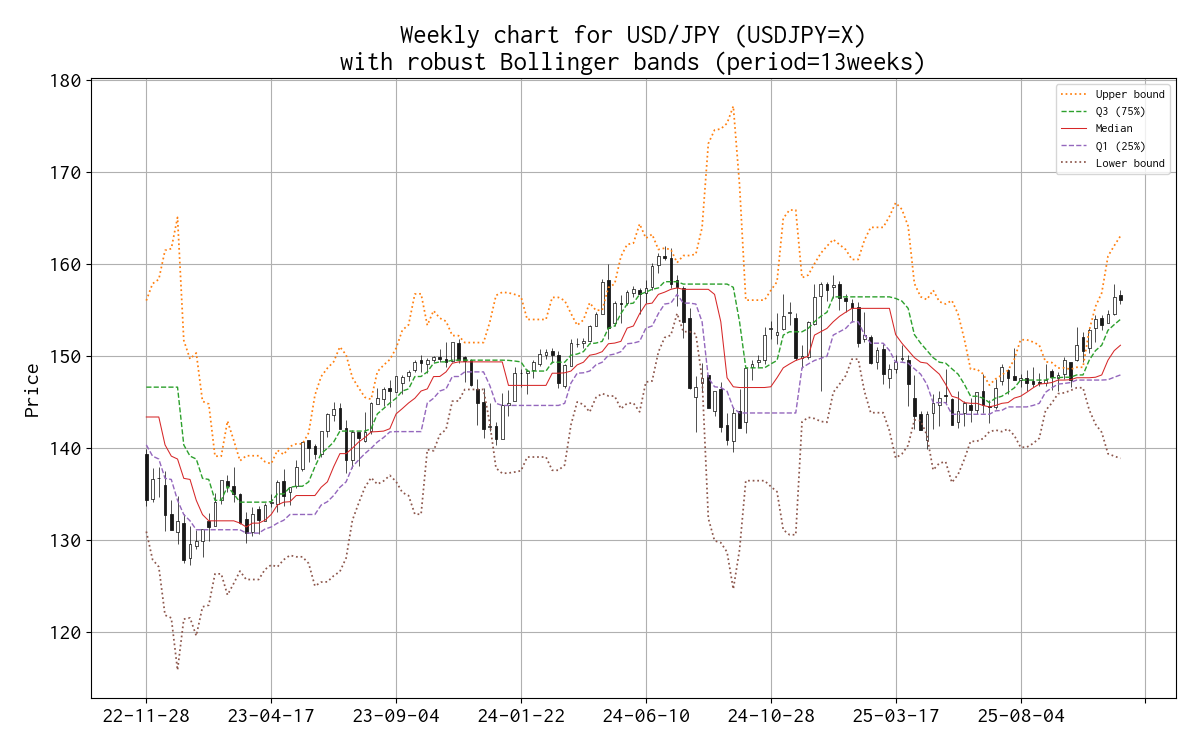
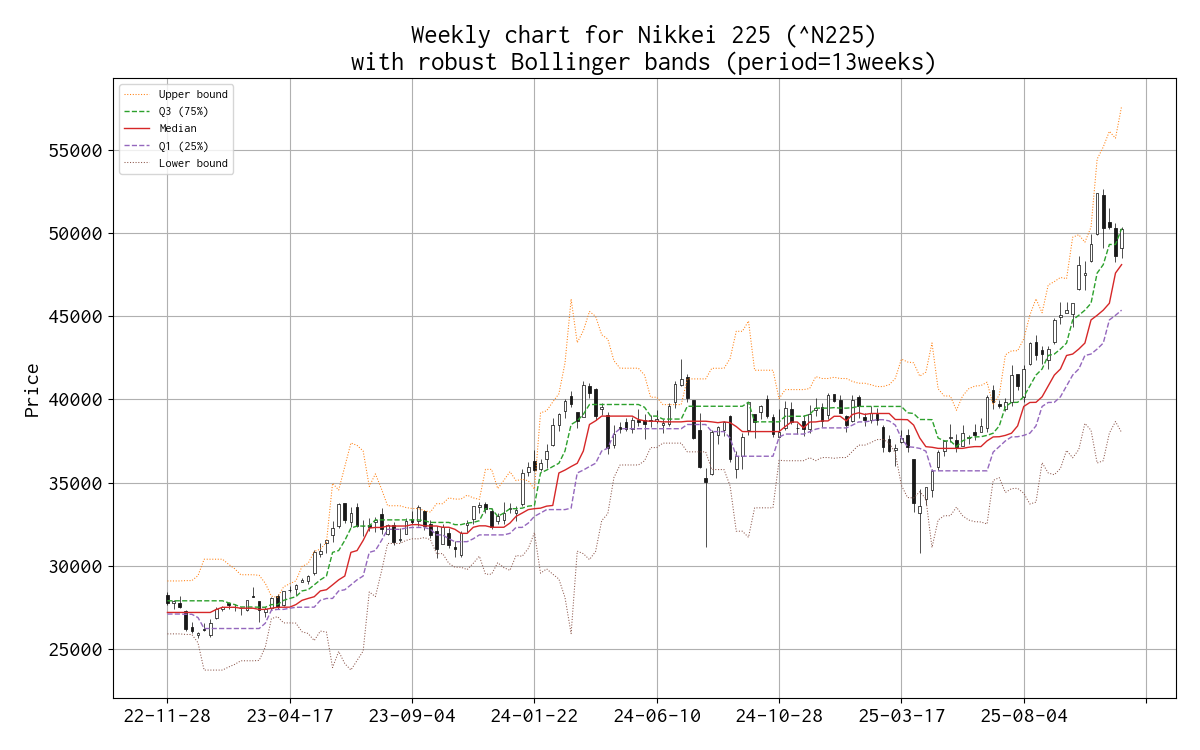
平均と標準偏差を、median と IQR(Q1 25% と Q3 75%)に置き換えたボリンジャーバンド(勝手に robust Bollinger bands と呼んでいます)のチャートを示しました。
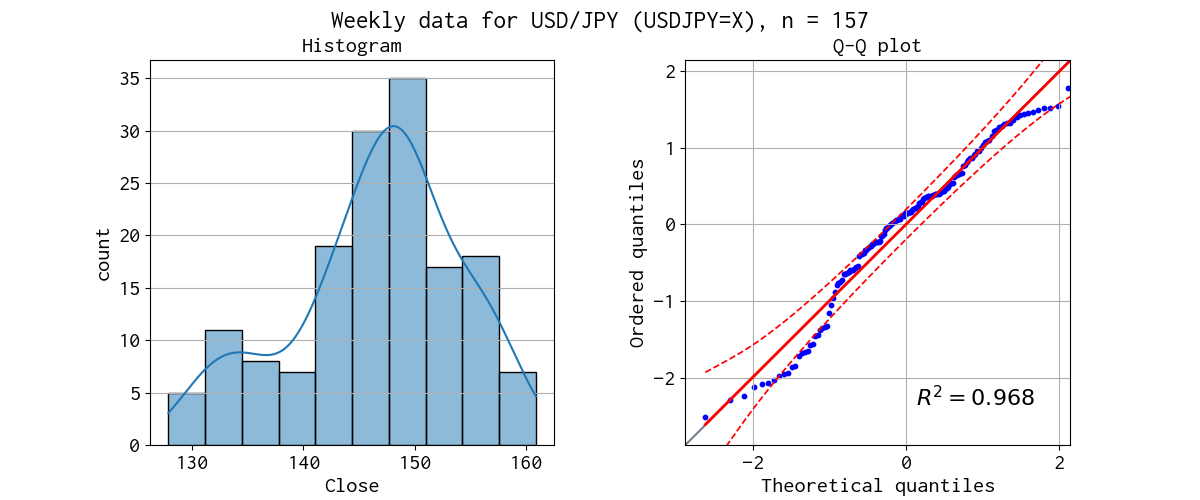
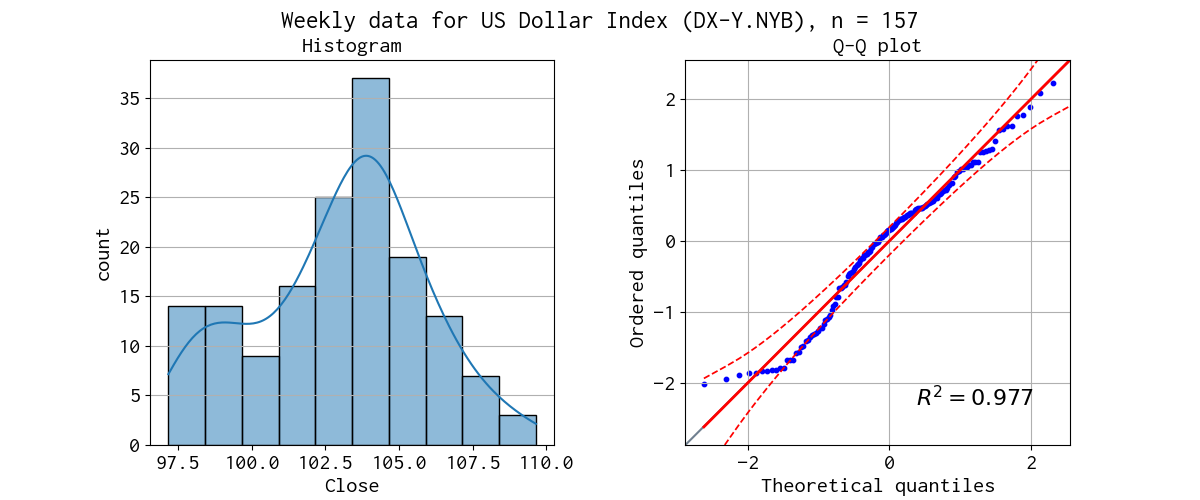
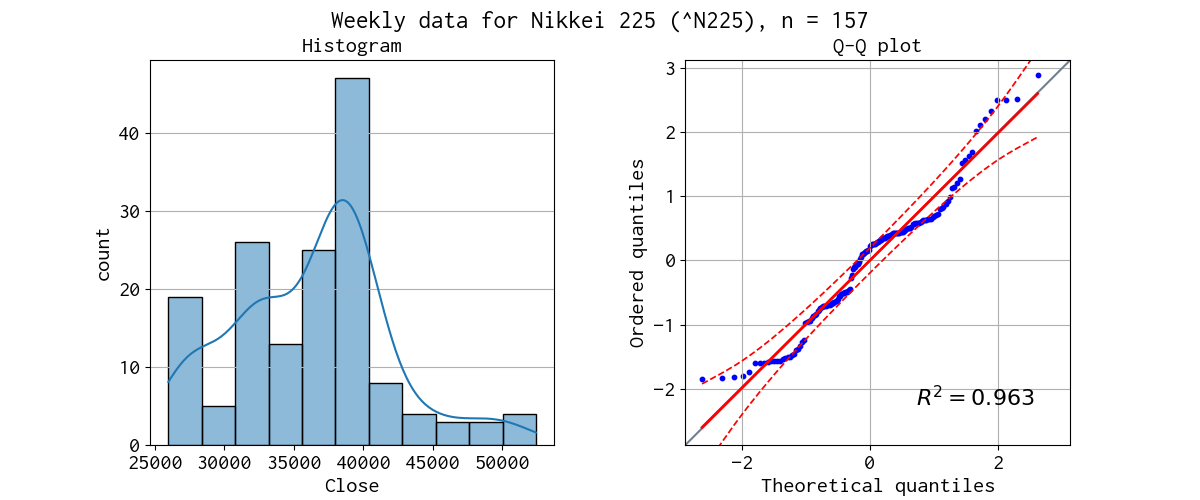
対象データのヒストグラムと Q-Q プロットを示しました。
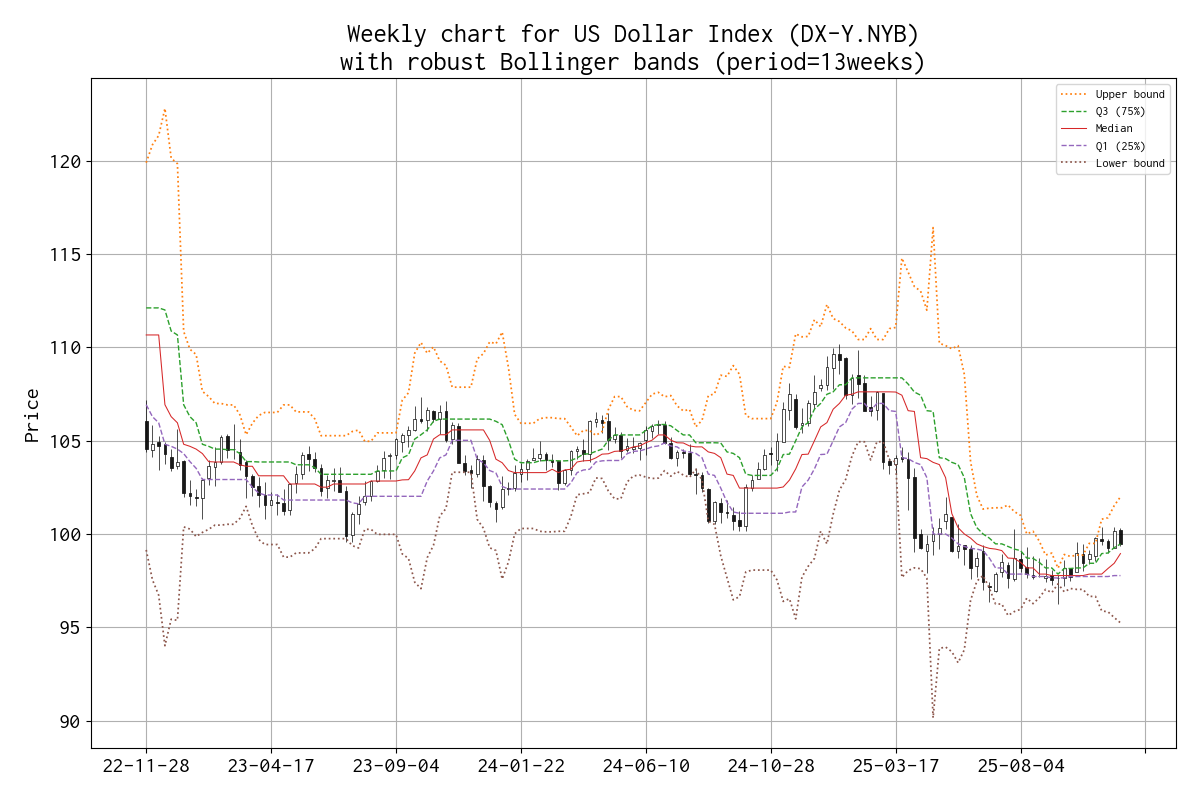
ドル指数
ドル指数 [2] のトレンドとボリンジャーバンドのチャートも示しました。
対象データのヒストグラムと Q-Q プロットを示しました。
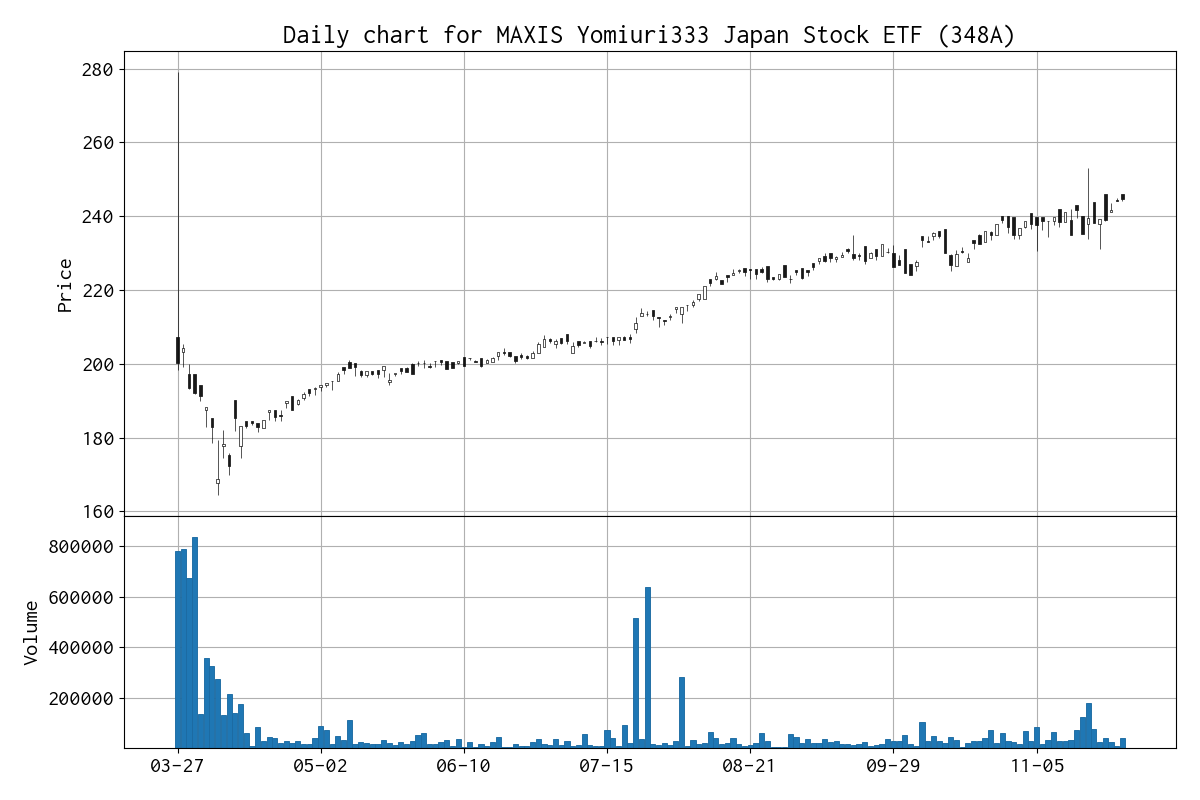
ローソク足チャートは Yahoo Finance のデータを利用して作成しました。
参考サイト
- 私の株日記: 標準偏差を使う気持ち悪さ [2025-03-16]
- ドル指数とは 基軸通貨の総合的な強さを指数化 - 日本経済新聞 [2025-04-19]